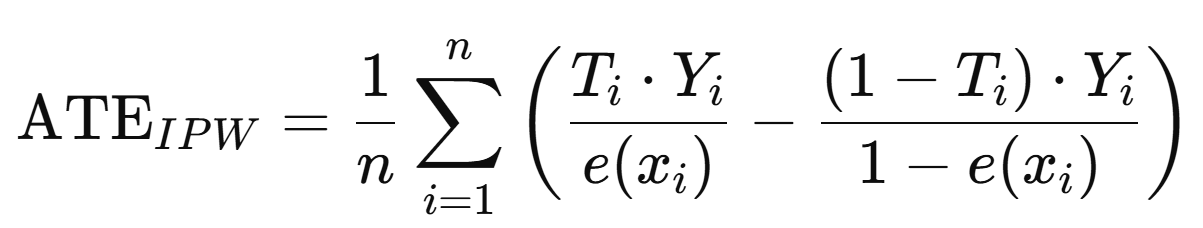Estimating Treatment Effects with IPW: A Guide for Data Scientists

Inverse Propensity Weighting is a powerful technique for estimating causal effects when typical AB experiments are not possible. In this blog, we break down the method, how it works, & when to use it.

and

May 20, 2025

👋 Hey! This is Manisha Arora from PrepVector. Welcome to the Tech Growth Series, a newsletter that aims to bridge the gap between academic knowledge and practical aspects of data science. My goal is to simplify complicated data concepts, share my perspectives on the latest trends, and share my learnings from building and leading data teams.

About the Authors:

Manisha Arora: Manisha is a Data Science Lead at Google Ads, where she leads the Measurement & Incrementality vertical across Search, YouTube, and Shopping. She has 12+ years of experience in enabling data-driven decision-making for product growth.

Banani Mohapatra: Banani is a seasoned data science product leader with over 12 years of experience across e-commerce, payments, and real estate domains. She currently leads a data science team for Walmart’s subscription product, driving growth while supporting fraud prevention and payment optimization. She is known for translating complex data into strategic solutions that accelerate business outcomes.

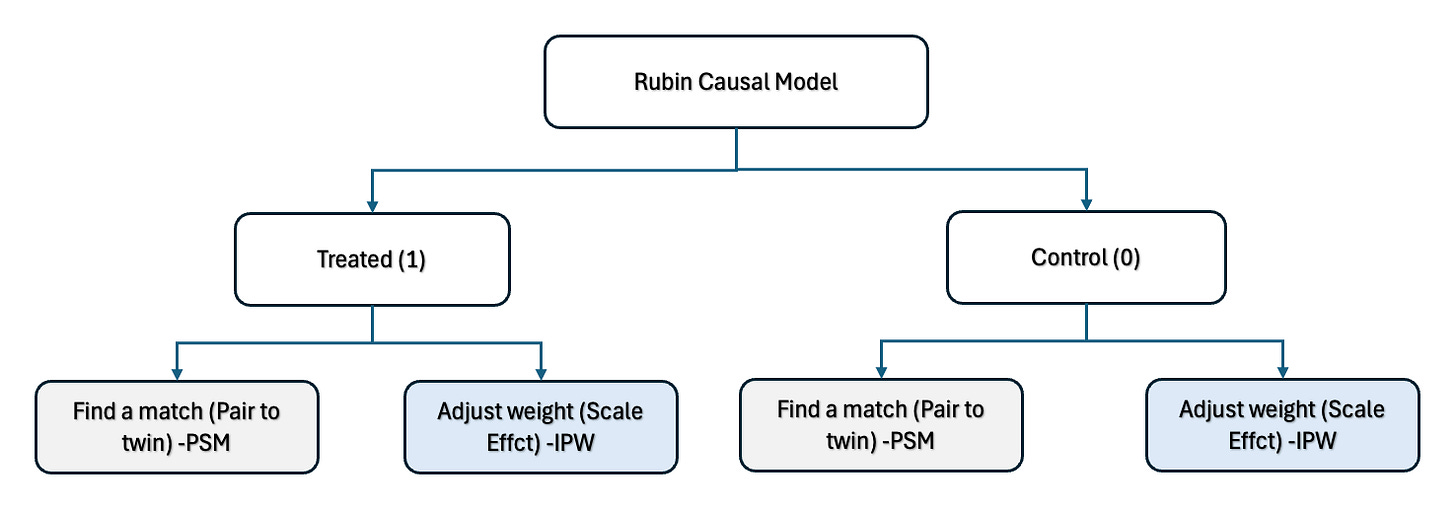
In our last post, we explored Propensity Score Matching (PSM)—a technique rooted in Rubin’s Potential Outcomes Framework. At its heart of the framework lies a simple but powerful idea:

For each individual, there are two potential outcomes—one if they receive the treatment, and one if they don’t.

In an ideal scenario, we’d run an A/B test every time we wanted to understand the impact of a new feature—whether it's free shipping, a recommendation tweak, or a change in pricing. But real-world constraints often make this hard:

Self-selection bias: Users opt in or out of a feature
Scaled rollout: A change was deployed globally with no control group
Ethical or operational constraints: You can’t withhold benefits from some users

As a result, we’re often stuck trying to answer causal questions using observational data - data where treatment wasn’t assigned at random. And that’s where things get tricky.

Imagine trying to measure the impact of a loyalty benefit, when users who engage more or spend more are also more likely to get the benefit in the first place. Any naïve comparison will conflate the treatment effect with these underlying differences.

This is the problem of confounding - when treatment and outcome are both influenced by other variables. Standard regression adjustments can’t always fix it, especially in high-dimensional or non-linear settings.

Here’s the challenge: for any given user, we can only observe one of these outcomes—never both. This is the fundamental problem of causal inference.

Methods like PSM and IPW are designed to overcome this problem using observational data—where treatments are not randomly assigned.

Refresher on Rubin’s framework assumes “strong ignorability”, meaning that:

Treatment assignment depends only on observed covariates (i.e., there are no unobserved confounders)
Every individual has a non-zero chance of receiving either treatment (positivity). If this holds, we can use the propensity score—the probability of receiving treatment given the covariates—as a tool to adjust for selection bias.

🧮 What Is IPW, and How Does It Work?

Inverse Probability Weighting (IPW) is a technique that lets us recreate the balance of a randomized experiment using observational data. The core idea is simple: if certain users were more likely to receive a treatment, we give them less weight when estimating the treatment effect—and vice versa.

IPW reweights the dataset so that the distribution of covariates is balanced across treatment groups, as if users had been randomly assigned.

Treated users with low propensity scores (i.e., unlikely to be treated) get higher weights, because they are rare and carry more information.
Control users with high propensity scores (i.e., likely to be treated but weren’t) also get higher weights, for the same reason.

By applying these inverse probabilities as weights, we create a “pseudo-population” where treatment assignment is independent of covariates—mimicking a randomized trial.

Step-by-Step Methodology:

1. Estimate Propensity Scores

We first build a model to estimate the propensity score—the probability that a user receives the treatment, given their covariates.

e(x) = P(Treatment = 1 | X = x)

For example, suppose we’re evaluating the impact of a free shipping benefit, and users with high purchase volume are more likely to receive it. The propensity score model will capture that.

2. Assign Weights Based on Propensity

We then assign a weight to each observation based on the inverse of the probability of receiving the treatment they actually got:

Treated users: 1 / e(x)
Untreated users: 1 / (1-e(x))

This reweights the data to simulate a population where treatment was randomly assigned.

In essence, we’re upweighting users who look like they could’ve gone either way, and downweighting those who were almost guaranteed to get treated.

3. Estimate the Average Treatment Effect (ATE)

Once weights are applied, we can use them to compute a weighted average of the outcomes across treated and untreated groups. The difference gives us the estimated causal effect.

This adjustment ensures that comparisons between the groups aren’t biased by differences in covariates.

When Should You Use IPW?

IPW is one of several tools in the causal inference toolbox. It’s not always the best tool—but in the right context, it can outperform traditional matching or regression-based approaches. So when should you use it?

✅ 1. When You Have Good Overlap but Large Imbalance

IPW works well when there's sufficient overlap in covariates between treated and untreated users, but the distribution is imbalanced. Instead of discarding data (like in matching), IPW lets you keep all users by reweighting them to simulate a balanced population.

IPW works well when there's sufficient overlap in covariates between treated and untreated users, but the distribution is imbalanced.

Example:
In a recommendation system rollout, say power users (who are very active) are far more likely to receive personalized recommendations. Matching would throw away many non-power users. IPW can retain all observations while correcting for this imbalance.

✅ 2. When You Want to Estimate Population-Level Effects

IPW gives you an estimate of the Average Treatment Effect (ATE)—how the treatment would affect the entire population if applied to everyone. This is useful in scenarios where you’re planning a broad rollout and care about overall lift.

Example:
You're deciding whether to offer free shipping to all users in your subscription program. IPW helps you model what would happen if everyone received the benefit, not just a specific segment.

IPW helps you model what would happen if everyone received the benefit, not just a specific segment.

We will cover this example in greater depth in the next blog.

Shameless plugs:

Product Data Science
Master Product Sense and AB Testing, and learn to use statistical methods to drive product growth. I focus on inculcating a problem-solving mindset, and application of data-driven strategies, including A/B Testing, ML, and Causal Inference, to drive product growth.

Check Out Product DS Course

AI/ML Projects for Data Professionals
Gain hands-on experience and build a portfolio of industry AI/ML projects. Scope ML Projects, get stakeholder buy-in, and execute the workflow from data exploration to model deployment. You will learn to use coding best practices to solve end-to-end AI and ML Projects to showcase to the employer or clients.

⚠️ When Not to Use IPW?

Poor Overlap: If treated and control groups are too different (i.e., extreme propensity scores close to 0 or 1), IPW can assign huge weights, increasing variance and making your estimates unstable.
Small Sample Sizes: IPW tends to be more variance-prone than matching, especially in small datasets.
Highly Correlated Covariates: IPW can become unstable when many covariates are tightly correlated, unless regularization or dimensionality reduction is applied.

PSM vs IPW vs Regression

⚠️ Caution & Diagnostics

Inverse Probability Weighting (IPW) is a powerful tool—but only if applied with care. Here’s how to ensure you're not flying blind:

✅ Check the distribution of weights

After computing IPW weights, plot a histogram to inspect their distribution.
Extremely large weights (often caused by propensity scores near 0 or 1) can overly influence your estimate and increase variance.

If a handful of users are contributing disproportionately, that’s a red flag.

✅ Evaluate covariate balance post-weighting

The goal of IPW is to balance covariates between treated and control groups.
Use metrics like standardized mean differences (SMDs) to evaluate whether weighting improved balance.
SMDs < 0.1 for most covariates generally indicate good balance.

✅ Use stabilized or truncated weights

Stabilized weights can reduce variance by keeping weights within a more reasonable range.
Truncation involves capping extreme weights—e.g., setting a max threshold (say, the 99th percentile).

These techniques help reduce the influence of outliers and make your causal estimates more robust.

What’s Next?

In this edition, we explored how IPW helps estimate causal effects when randomization isn't feasible. We’ll walk through a real-world example, applying IPW using Python and interpreting the results.

Upcoming Courses:

Product Data Science
Master Product Sense and AB Testing, and learn to use statistical methods to drive product growth. I focus on inculcating a problem-solving mindset, and application of data-driven strategies, including A/B Testing, ML, and Causal Inference, to drive product growth.